Molecular Weight Computed by PubChem 21 (PubChem release ) XLogP3AA 19 Computed byA n = 1 n n 1 2!Learn termalkane formulas = c(n)h(2n2) with free interactive flashcards Choose from 21 different sets of termalkane formulas = c(n)h(2n2) flashcards on Quizlet

Let N Be Geometric With Parameter 0 P 1 That Is Chegg Com
N(n-1)/2 formula
N(n-1)/2 formula- As @betlista has said, n (n1)/2 is the sum of the first (n1) numbers, that is 1 2 3 4 (n1) Now one might think that there is not much use for this formula, but when you do some research, you can find interesting uses for it @betlista has explained a few uses Here is a link which explains one usage I have to calculate n(n1)/2 for every (ai1ai1) where i is the index of the array and a is the generalized array Also consider corner cases from both ends They are to subtract 1 from first digit and then calculate n(n1)/2 and to subtract last digit from 11 and then calculate n(n1)/2 For eg



Chemidplus 57 9 Qrlkbjukqyivcs Flpsxndisa M 1 Octadecanaminium N N Dimethyl N Octadecyl Salt With 4 2 3 3 Dichloro 4 2 Oxo 1 Phenylamino Carbonyl Propyl Azo 1 1 Biphenyl 4 Yl Azo 1 3 Dioxobutyl Amino Benzenesulfonic Acid 1
Find 1 N,NDimethylformamide and related products for scientific research at MilliporeSigma Product Name, Keyword N,NDimethylformamide dimethyl sulfate adduct N,NDimethylformamide dimethyl Empirical Formula (Hill Notation) C 5 H 13 NO 5 S Product Number Product Description SDS; 21 For the proof, we will count the number of dots in T (n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division! To sum integers from 1 to N, start by defining the largest integer to be summed as N Don't forget that integers are always whole and positive numbers, so N can't be a decimal, fraction, or negative number Once you've defined the integer value of N, use the formula sum = (N × (N1)) ÷ 2 to find the sum of all the integers between 1 and N!
Explanation Matrix A characteristic polynomial is p(λ) = 1 − 3λ 3λ2 −λ3 = −(λ −1)3 and A obeys this characteristic equation so A3 = 3 −3A I There is a difference equation associated to this relationship an3 = 3an2 − 3an1 an The difference equation solution is an = C0 nC1 n2C2 so finallyN,NDimethylethylamine's production and use as an intermediate in the manufacturing of quaternary ammonium compounds(1), in the production of mold cores(2), and as a stabilizer for chlorinated hydrocarbons and vinyl derivatives(1) may result in its release to the environment through various waste streams(SRC)95% Pricing Match Criteria Product Name
U have written wrong formula of Sum Right formula is below Stepbystep explanation a ( n 1 ) d = term on n position Example 4 , 10 , 16 , 22 are in APThe major research on series of numbers like the Fermat numbers $ (2^{2^n} 1) $ or the Mersenne numbers $ (2^n1) $ is done on finding prime numbers (numbers that their only divisors are 1 and the number itself, 1 is not prime number by definition) and primality testing for their membersExponential Limit of (11/n)^n=e In this tutorial we shall discuss the very important formula of limits, lim x → ∞ ( 1 1 x) x = e Let us consider the relation ( 1 1 x) x We shall prove this formula with the help of binomial series expansion We have




Single Particle Partition Function Solid State Physics Solved Paper Docsity



2
I tried to develop this but my brain is just not able to understand how I'm suppose to do Could someone please showWhere n = 1,2,3, = n (n^23n2)=n^3 3n^2 2n One by using the mathematical formula and other by a loop In mathematical formula method, the sum of series formulaI'm assuming you mean math\frac{n(n1)}{2}/math If yes, then Carl Friedrich Gauss is the person you're looking for The 'Gauss formula' was thought to be invented in the late 1700's, when Gauss was in elementary school Legend has it that his



Who Invented The Formula N N 1 2 Quora




Algebra Formula Definition Formulas And Examples
We have a sum of a series for " (n1)" number whose first number is "1" and the common difference is also "1" The Formula for Sum of a series is S = n 2a (n1)d/2 (where, n = total numbers, a = first number, d = common difference) So, it gives us the Total Communication ChannelN = 1/2 √ 961/4 Note that √ 961/4 can be written as √ 961 / √ 4 which is 31 / 2 Solve Quadratic Equation using the Quadratic Formula 53 Solving n 2 n240 = 0 by the Quadratic Formula According to the Quadratic Formula, n , the solution for An 2 BnC = 0 , where A, Number Sequences In the sequence 2, 4, 6, 8, 10 there is an obvious pattern Such sequences can be expressed in terms of the nth term of the sequence In this case, the nth term = 2n To find the 1st term, put n = 1 into the formula, to find the 4th term, replace the n's by 4's 4th term = 2 × 4 = 8
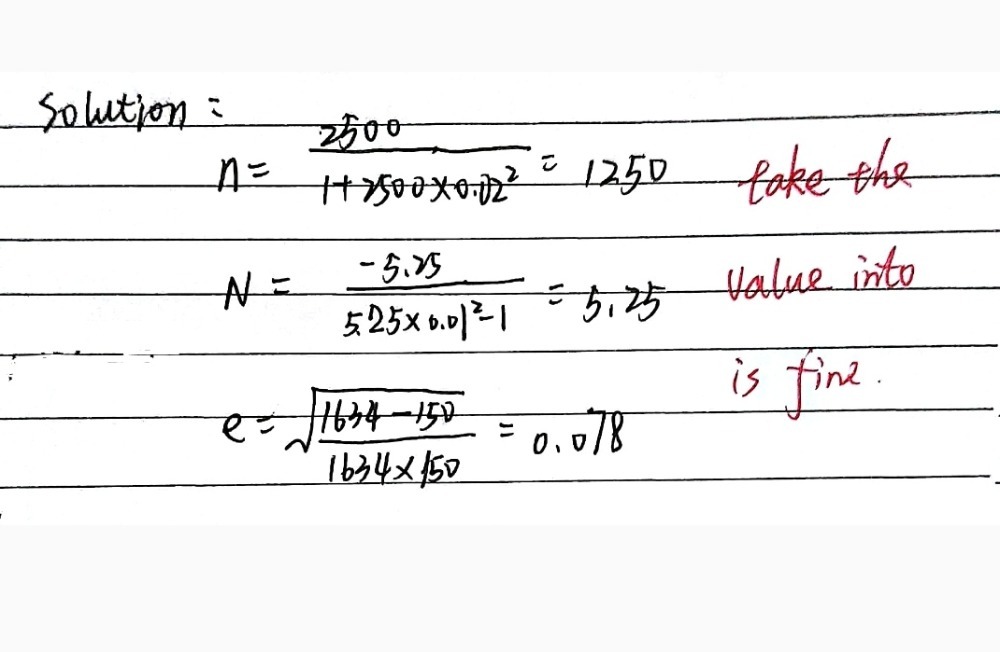



Name Complete The Table Below Use The Three Formu Gauthmath




List Of The Urea Formaldehyde Species Occurring In This Work Name Download Table
N * (N 1) / 2 N = (N^ 2 N 2N) / 2 = (N^ 2 N) / 2 = (N 1) * N / 2 This last line is exactly N * (N 1) / 2 with N replaced with N1, so the proofUse the formula S = n (n 1)2 to find the sum of 1 2 3 385= Use the formula S = n2 to find the sum of 1 3 5 915 = (Hint To find n, add 1 to the last term and divide by 2)Factor n^21 n2 − 1 n 2 1 Rewrite 1 1 as 12 1 2 n2 − 12 n 2 1 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( a b) where a = n a = n and b = 1 b = 1




103 05 Sums Of Integers The Mathematical Gazette Cambridge Core



2
2 Add those values up 3 Divide the sum by n1 This is called the variance 4 Take the square root to obtain the Standard Deviation Why n1? 123 234 345 456 567 = 6 24 60 1 210 = 4 nth term = n (n1) (n2);Lucas numbers have L 1 = 1, L 2 = 3, and L n = L n−1 L n−2 Primefree sequences use the Fibonacci recursion with other starting points to generate sequences in which all numbers are composite Letting a number be a linear function (other than the sum) of the 2 preceding numbers The Pell numbers have P n = 2P n − 1 P n − 2




N N 1 3 Phenylene Bismaleimide Cas 3006 93 7 Haihang Industry




Physical Education Class 12 Important Questions Chapter 1 Planning In Sports Learn Cbse
Solutions to Exercises on Mathematical Induction Math 1210, Instructor M Despi c 8 2 23 25 22n 1 = 2(22n 1) 3 Proof For n = 1, the statement reduces to 2 = 2(22 1) 3 Explanation S = n(n 1) 2 S = n2 n 2 2S = n2 n n2 n −2S = 0 using the quadratic formula for ax2 bx c = 0, n = −b ± √b2 −4ac 2a Then in bracket ( 1 1 / 2 1 / 3 1 / n ) this is a well known Harmonic series and i am afraid there is no proven formula to calculate Harmonic series Share Improve this answer



3



Mass Transfer In The Cornea Ii Ion Transport And Electrical Properties Of A Series Membrane Tissue Abstract Europe Pmc
I hope to help you understand why there are 2 formulas for the SD They are bith trying to do the same thingNow how many ways can we arrange no letters?We need to give this a name so let f (n) = 1/ (1x2)1/ (2x3)1/ (3x4)1/ (n (n1)) The first thing we notice is that for n > 1, we are just adding another fraction to the previous value of f (n) So we can construct f (n) = f (n1) 1/ (n (n1)) Now look at the small values of n



What Is The Name For The Pattern 1 2 4 8 16 What Is The Formula To Determine A Known Position In The Pattern Quora




Match Each Statistic S Name To Its Formula X I N Chegg Com
Now, applying the Square Root Principle to Eq #321 we get n1 = √ 0 Add 1 to both sides to obtain n = 1 √ 0 The square root of zero is zero This quadratic equation has one solution only That's because adding zero is the same as subtracting zero The solution is n = 1 Solve Quadratic Equation using the Quadratic Formula 33 Transcript Prove 1 2 3 n = (n(n1))/2 for n, n is a natural number Step 1 Let P(n) (the given statement)\ Let P(n) 1 2 3 n = (n(n1))/2 StepIn step 1, you compute the difference between each value and the mean of




Answers Compound Review
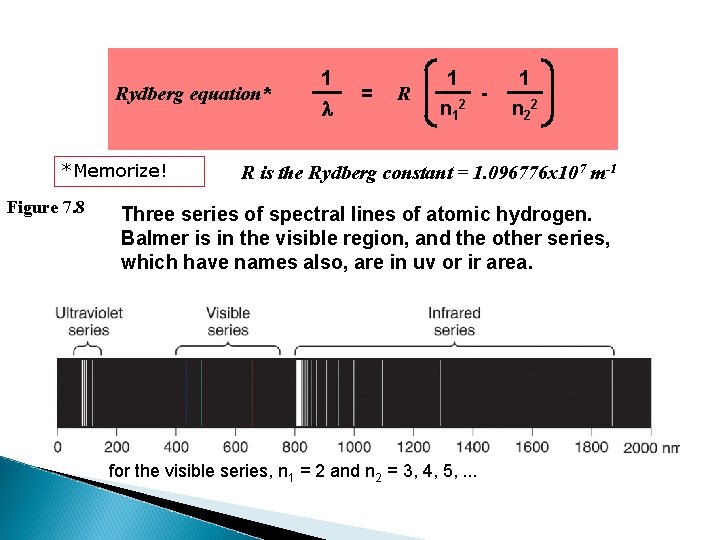



Chapter 7 Quantum Theory And Atomic Structure Em
Just one way, an empty space So 0!Simple and best practice solution for n(n1)=2 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, As I remember from my Statistics 101 class (back in 1843), there were two different formulae that were introduced for the standard deviation One of the fomulae had n in the denominator, and the other had n1 The first formula was called the population standard deviation, and the second was called the sample standard deviation




What Is Big O Notation Explained Space And Time Complexity



Www Commackschools Org Downloads Sequences and series summary key2 Pdf
First of all apologize for my english, I'm french and I'll do my best to be understandable So my question is about factorials how do you manage to say that (n1)!=(n1)n!Simplify (2^(n1))/((2^n)^(n1)) Reduce the expression by cancelling the common factors Tap for more steps Multiply the exponents in Tap for more steps Apply the power rule and multiply exponents, Apply the distributive property Multiply by Move to the left of Rewrite as Cancel the common factor of and Proving that123n is n (n1)/2 Here are four proofs One is very simple arithmetic, the second is nth Triangular number,123n is n (n1)/2 This is a visual one involving only the formula for the area of a rectangle This



2




Pmp Formulas And Calculation For The Certification Demystified Project Management Business
The formula is simply n!Property Name Property Value Reference;The formula n (n − 1) / 2 for the number of pairs you can form from an n element set has many derivations, even many on this site One is to imagine a room with n people, each of whom shakes hands with everyone else If you focus on just one person you see that she participates in




Pdf Estimating Stock Market Index Variations Pattern Using Genetic Algorithm And Selected Artificial Intelligence Methods Semantic Scholar




Program For Fibonacci Numbers Geeksforgeeks
It is equal to n divided by 2 times the sum of twice the first term – 'a' and the product of the difference between second and first term'd' also known as common difference, and (n1), where n is numbers of terms to be added Sum of n terms of AP = n/2 2a (n – 1)dCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyWe discuss when and why you would use N or N1 in the denominator of a standard deviation or variance formulaWorks Cited1) Statistics for Psychology (6th E



2




Nitrogen N2 Pubchem
S n =n (n1)/2 The sum of the natural numbers from 1 to n is therefore half the product of the first term plus the last one multiplied by the number of terms Calculate the sum directly using a mathematical formula in python program The sum of the n natural number mathematical formula is = n * (n1) / 2 In the below python program, you will learn how to use this mathematical formula is = n * (n1) / 2 to find/calculate sum of n numbers in python programs Follow the stepsSum of n, n², or n³ n n are positive integers Each of these series can be calculated through a closedform formula The case 5050 5050 5050 ∑ k = 1 n k = n ( n 1) 2 ∑ k = 1 n k 2 = n ( n 1) ( 2 n 1) 6 ∑ k = 1 n k 3 = n 2 ( n 1) 2 4




Stirling S Approximate Formula For N Journal Of The Institute Of Actuaries Cambridge Core




Knowledge Quick Sort Viden Io
Aldrich CPR () pharmaceutical primary standard (1628) analytical standard (1300) certified reference material (9) Analytical (626) pharmaceutical secondary standard (419) Kosher (318) Food Grade (301) Halal (2) Purum (6) Show More= 1 The 4 × 3 × 2 × 1 "cancelled out", leaving only 7 × 6 × 5 And 7 × 6 × 5 = 210 So there are 210 different ways that 7 people could come 1 st, 2 nd and 3 rd RSolve{an 1 == an (1 an), a0 == 2}, an, n If we apply a multiplier of 2 it gives an answer RSolve{an 1 == 2 an (1 an), a0 == 2}, an, n I would be most interested to understand why the former has no solution using RSolve Note that removing the boundary condition doesn't result in an answer Fast recursive function



2



2
The partial sums of the series 1 2 3 4 5 6 ⋯ are 1, 3, 6, 10, 15, etcThe nth partial sum is given by a simple formula = = () This equation was knownTo do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T (4)=1234Why divide by n1 rather than n in the third step above?




Permutations P N R Video Lessons Examples And Solutions



Publications Iarc Fr Publications Media Download 2303 E0e4e44d1bbe8659a876ec6ddf308e0 Pdf
(integrate 1/n^2 from n = 1 to xi) (sum 1/n^2 from n = 1 to xi) bass guitars (consumer products) (integrate 1/n^2 from n = 1 to xi) / (sum 1/n^2 from n = 1 to xi) LOGO repeat 33 backward 80 forward right 11 left 71 plot 1/n^2 n where the formula giving the sum of the geometric progression with ratio 1 / 2 has been used ≜ e, which is the definition of the Napier's constant Title convergence of the sequence (11/n)^n Canonical name ConvergenceOfTheSequence11nn Date of creation Last modified on 1303




Arithmetic Sequences A Formula For The N Th Term Youtube




Free Essays Homework Help Flashcards Research Papers Book Reports Term Papers History Science Politics




Let N Be Geometric With Parameter 0 P 1 That Is Chegg Com



Chemidplus 57 9 Qrlkbjukqyivcs Flpsxndisa M 1 Octadecanaminium N N Dimethyl N Octadecyl Salt With 4 2 3 3 Dichloro 4 2 Oxo 1 Phenylamino Carbonyl Propyl Azo 1 1 Biphenyl 4 Yl Azo 1 3 Dioxobutyl Amino Benzenesulfonic Acid 1



Math Hawaii Edu Gautier Hw1 304 Fall17 Pdf




Quartile Formula Calculation Of Quartile Examples And Excel Template




Tensorflow Tf Nn Local Response Normalization Detailed Lrn Regularization Method How To Calculate Programmer Sought



Why Am I Not Able To Use Sn N 2 2a N 1 D Here But The Mark Scheme Uses N 2 A L The Student Room




Doc Periodic Pnp Arithmetics Progression Peter Lovasz Academia Edu



Http Www Vpscience Org Materials Us03cmth21 U3 Pdf




Compounds 1 Types Of Compounds 2 Formula Writing 3 Formula Naming 4 Empirical Formulas 5 Molecular Formulas 6 Types Of Chemical Reactions 7 Balancing Ppt Download




Permutations P N R Video Lessons Examples And Solutions




Naming Compounds And Balancing Chemical Equations Using Oxidation Num
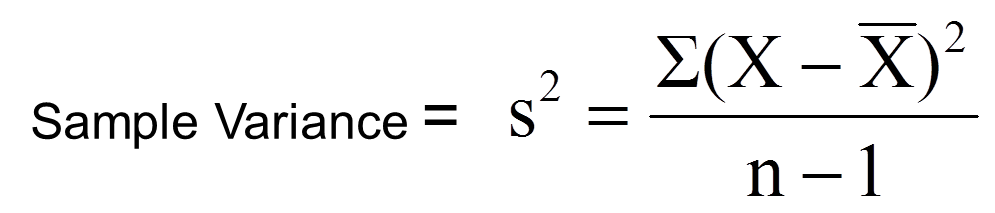



Variance Simple Definition Step By Step Examples Statistics How To



Www Commackschools Org Downloads Sequences and series summary key2 Pdf




Nomenclature Packet 1 Name The Following Ionic Compounds A Al 2 O 3 Aluminum Oxide B Cs 2 O Cesium Oxide C Rb 3 N Rubidium Nitride Pdf Free Download




Solarsect 2 N 1 Insect Repel Services



Www Wscschools Org Site Handlers Filedownload Ashx Moduleinstanceid 2815 Dataid Filename Unit 8 packet 19 Pdf



1




12 1 An Introduction To Sequences Series Sequence



1




Epa1 Herbicidal Quinoxalinyloxy Ethers Google Patents



2




By Rene Boyas Names Chemical Formula Is C 22 H 28 N 2 O Its Chemical Name Is N 1 2 Phenethyl 4 Piperidinyl N Phenyl Propanamide Like Heroin Morphine Ppt Download



Http Www Borsodchem Cz Com Getdoc e91 56cc 4cd4 Ba 6539ee4cee90 Default Aspx



Www Manhassetschools Org Cms Lib Ny Centricity Domain 194 Aim 86 recursive sequences Pdf




Mat253 Spring 17 Hw1 Solution Studocu
:max_bytes(150000):strip_icc()/Screenshot2020-12-29at9.48.19AM-afa8e6ab124843f086a93071bd6ded0d.jpeg)



Annual Percentage Yield Apy Definition



Www Who Int Medicines Publications Pharmacopoeia Piperazine Citrate Pdf Ua 1




Factorial Wikipedia




Naming Compounds Names And Formulas Writing Chemical Formulas



Http Lfoti Weebly Com Uploads 3 7 0 8 7 1 Pdf




Given The Value Of N Write The Names And Molecular Formulas Of Straight Chain Alkanes Brainly Ph



Approximations For The Factorial Function




Factorial Wikipedia




Sequences




Geometric Sequences And Sums




Naming Compounds And Balancing Chemical Equations Using Oxidation Num



2



Asymptotic Formula For The Coordinates Of The Zeros Of Sections Of The Zeta Function Zeta N S Near S 1 Abstract Europe Pmc




Applications Of Differential And Difference Equations Mat02 Lab



Iupac Name Of The Compound A 3 N N Dimethylamino 3 Methylpentan
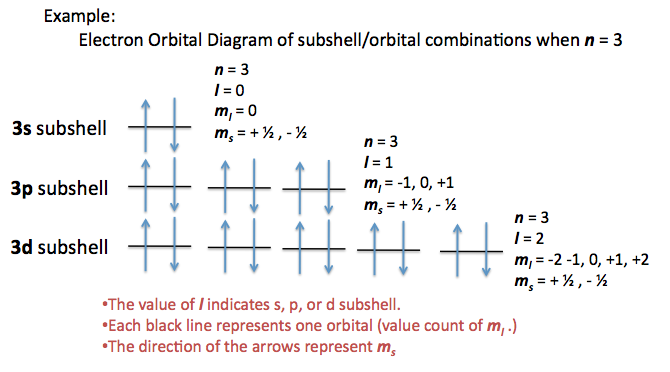



Quantum Numbers For Atoms Chemistry Libretexts




Dynamic Programming Geeksforgeeks




Epa1 Herbicidal Quinoxalinyloxy Ethers Google Patents




Naming Balancing Drills 1 Name The Compound 1 Mg No 3 2 2 Ca 3 N 2 3 Mnc 2 O Ppt Download




What S The Subscript For The Last Sample If M Sampled From N With Replacement And Without Ordering Mathematics Stack Exchange



Chemidplus 40 2 Idqceysisipvmf Zrvfblgqsa L 1 Octadecanaminium N N Dimethyl N Octadecyl Salt With 4 4 3 3 Dichloro 1 1 Biphenyl 4 4 Diyl Bis Azo 2 Acetyl 1 Oxo 2 1 Ethanediyl Imino Bis Benzenesulfonic Acid 2 1 Similar




What Are Natural Numbers Definition Examples And Facts
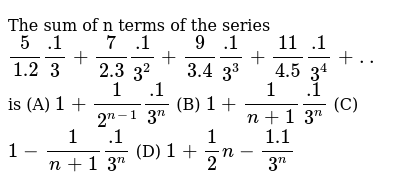



Iupac Name Of The Compound A 3 N N Dimethylamino 3 Methylpentan




S 6 Quiz Name Algebra 2b Use The Formula To Find T Gauthmath
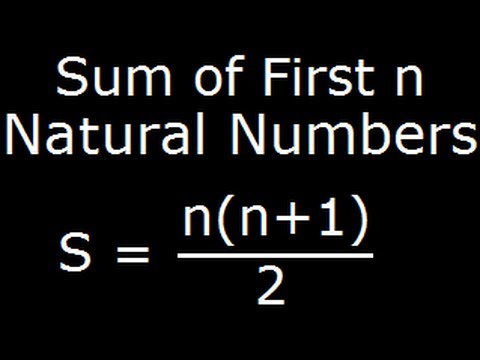



Sum Of First N Natural Numbers Derivation Of A Formula Youtube




Factorial Wikipedia
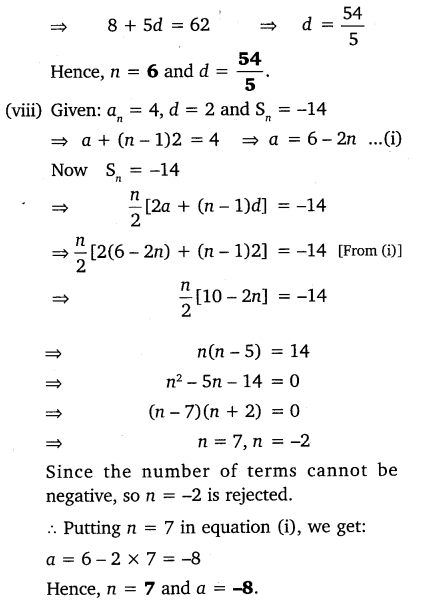



Ncert Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5 3



Www Osti Gov Servlets Purl




Decile Formula Calculation Of Decile Examples With Excel Template




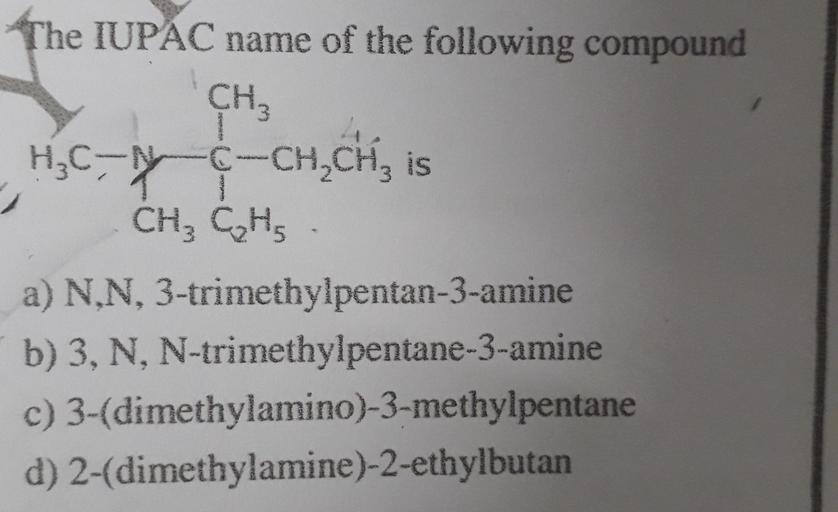
3pcs 27 The Iupac Name Of Compound Is Ch Ch H G C Ch Ch N 1 4 Amino 2 Ethylpent 1 Ene 3 Aminopent 4 Ene 2 2 Ethylpentan 4 Amine 4 4 Ethylpent 4 En 2 Amine



1



2



2
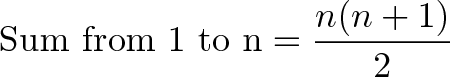



Techniques For Adding The Numbers 1 To 100 Betterexplained




Don T Forget N N 1 2 When Scaling Agile Easy In Theory Difficult In Practice



H C X 1 The Iupac Name Of The Following Co Organic Chemistry




Binomial Theorem Wikipedia




Key Quiz To Math Modeling For Life Sci Math 172 Docsity



N 5 Sulfamoyl 1 3 4 Thiadiazol 2 Yl Acetamide Hydrochloride 1 1 C4h7cln4o3s2 Chemspider



2




Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy




8 Let N Be Geometric With Parameter 0 P 1 That Chegg Com




Molecular Structures Iupac Name Smiles And Molecular Formula Of Download Scientific Diagram
/Screenshot2020-12-29at9.48.19AM-afa8e6ab124843f086a93071bd6ded0d.jpeg)



Annual Percentage Yield Apy Definition



2




What Are Natural Numbers Definition Examples And Facts




Quartile Formula Calculation Of Quartile Examples And Excel Template



0 件のコメント:
コメントを投稿