Given that the leg opposite the 30° angle for a triangle has a length of 12, find the length of the other leg and the hypotenuse The hypotenuse is 2 × 12 =A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle ) Because the angles are always in that ratio, the sides are also always in the same ratio to each otherIn the study of trigonometry the 30 60 90 triangle is considered a special triangle knowing the ratio of the sides of a 30 60 90 triangle allows us to find the exact values of the three trigonometric functions sine cosine and tangent for the angles 30 and 60 Special right triangles 30 60 90 A 45 45 90 isosceles right triangle has a side 1
Special Right Triangle Wikipedia
What is the ratio for a 30 60 90 triangle
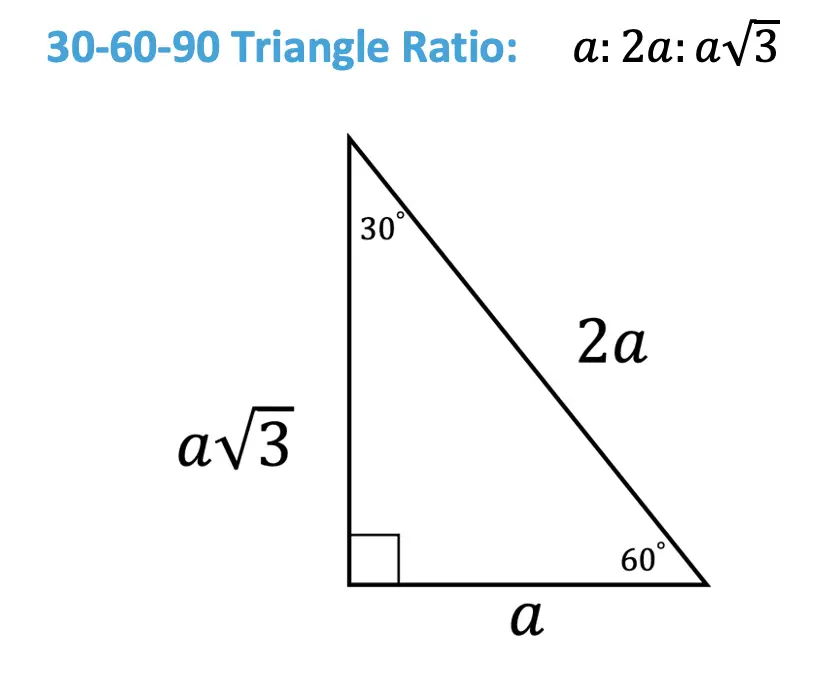
What is the ratio for a 30 60 90 triangle-The ratio of side lengths in such triangles is always the same if the leg opposite the 30 degree angle is of length x, the leg opposite the 60 degree angle will be of x, and the hypotenuse across from the right angle will be 2x Here is a triangle pictured below Figure % A triangle 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!




Instructions Use The Ratio Of A 30 60 90 Triangle To Solve For The Variables Leave Your Answers As Brainly Com
This is a special triangle It is like half an equilateral triangle The long side is equal to the sides of the equilateral triangle The base is half the long side and the altitude is the remaining side If x = short half side, which is opposite A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other The side opposite the 30º angle is the shortest and the length of it is usually labeled as x The side opposite the 60º angle has a Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another The basic triangle ratio is Side opposite the 30° angle x Side opposite the 60° angle x * √ 3 Side opposite the 90° angle 2 x
A triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 SEMATHS ORG A triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 Any triangle of the form can be solved without applying longstep methods such as the Pythagorean Theorem and trigonometric functionsThe 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progression The proof of this fact is simple and follows on from the fact that if α, α δ, α 2δ are the angles in the progression then the sum of the angles 3α 3δ =
Triangle Ratio A degree triangle is a special right triangle, so it's side lengths are always consistent with each other The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x xA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and How to solve triangles Definition of a triangles, including angles and side lengths A 3 0 − 6 0 − 9 0 3 0 − 6 0 − 9 0 is a scalene triangle and each side has a different measure



30 60 90 Triangle




Special Right Triangles Video Lessons Examples And Solutions
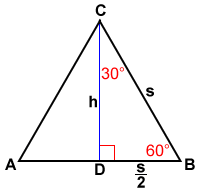
How would one find the other two sides of a rightangled triangle having angles 30°, 60°, and 90° if the hypotenuse of the triangle is 2m?How are they different?Here is the proof that in a 30°60°90° triangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90° triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60° (Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30° angles




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation



Identifying The 30 60 90 Degree Triangle Dummies
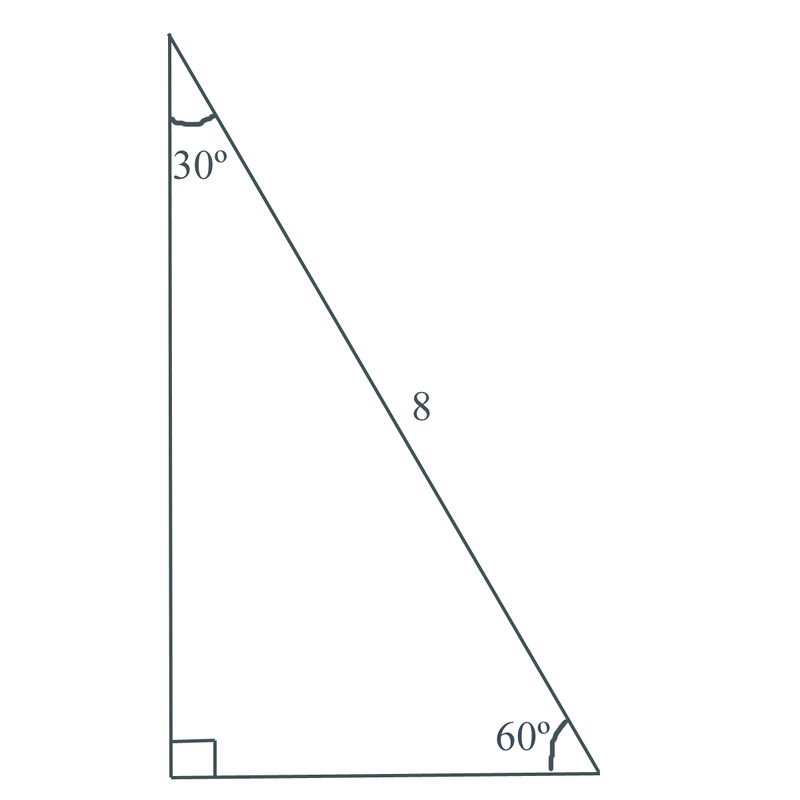
If you know the short leg length multiply by two for the hypotenuse length If you know the short leg then multiply by √3 for the long leg length If you know the long leg length divide by √3 for the short leg length The area of a triangle equals 1/2base * height2 n = 2 × 4 = 8 Answer The length of the hypotenuse is 8 inches You can also recognize a triangle by the angles As long as you know that one of the angles in the rightangle triangle is either 30° or 60° then it must be a special right triangleMultiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuse



30 60 90 Triangle



Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
It is an outline of what the candidate intends or proposes to achieve in the first 90 days, if hired for the role Similarly one may ask, what are the sides of a 30 60 90 Triangle?, Triangles Angles of Elevation and Depression and Word Problems pg 1 Using the side lengths in triangle ABC, find the following values based off of the 0 angle tan 0 = cos 0 = sin 0 = Trig Ratio Recap For a right triangle, the sine, cosine, and tangent of the angle e is defined as sin 9 — Remember cos 9 =Answer (1 of 3) In order to answer this question properly, we must first know how the concept of a 30°60°90° (obviously "right" as one angle is 90°) triangle is best encountered consider first an equilateral triangle All sides are the same length, by definition, and the three equal angles m




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




Special Right Triangles Fully Explained W 19 Examples
The 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sides By Rich Zwelling, Apex GMAT Instructor Date 7th January, 21 Right Triangle In a previous piece, we covered the right triangle, also known as the isosceles right triangleThere is another socalled "special right triangle" commonly tested on the GMAT, namely the right triangle Like the isosceles right, its sides always fit a specific ratio, The shortest and lengthiest side in any Triangle is always contrary to the smallest and largest angle This policy likewise relates to the triangle Triangle with the very same angle steps are comparable, and also, their sides will always remain in




30 60 90 Right Triangle Side Ratios Expii




30 60 90 Right Triangles Free Math Help
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degreesBecause it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherThis is a triangle in which the side lengths are in the ratio of x x√32x Substitute x = 7m for the longer leg and the hypotenuse ⇒ x √3 = 7√3 ⇒ 2x = 2 (7) =14 Hence, the other sides are 14m and 7√3m Example 6 In a right triangle, the hypotenuse is 12 cm, and the smaller angle isA triangle is a unique right triangle whose angles are 30º, 60º, and 90º The triangle is unique because its side sizes are always in the proportion of 1 √ 32 Any triangle of the kind can be fixed without applying longstep approaches such as the Pythagorean Theorem and trigonometric features



The Easy Guide To The 30 60 90 Triangle
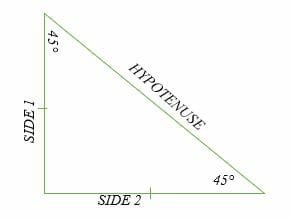



45 45 90 Triangle Explanation Examples
This means that the ratio of the lengths of the shortest side to the hypotenuse of any right triangle is 12 Therefore, If a triangle is a right triangle, the ratio of the sides (short leglong leghypotenuse) is 1√32We know from Plane (Euclidean) Geometry that in a right triangle, the length of the side opposite the 30 degree angle is equal to onehalf the length of the hypotenuse A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other The side opposite the 30º angle is the shortest and the length of it



Solution In A Triangle Abc Angle A 30 Angle B 90 And Ab Is 12 Cm Find The Length Of




Special Right Triangle Wikipedia
Example of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units in How are the proofs for the side length ratios of and triangles similar?Showing the ratios of the sides of a triangle are 11sqrt (2) Created by Sal Khan Special right triangles Special right triangles proof (part 1) Special right triangles proof (part 2) This is the currently selected item Practice Special right triangles triangle example problem Area of a regular hexagon




Special Right Triangles Proof Part 1 Video Khan Academy




Special Right Triangles Part 3 30 60 90 Youtube
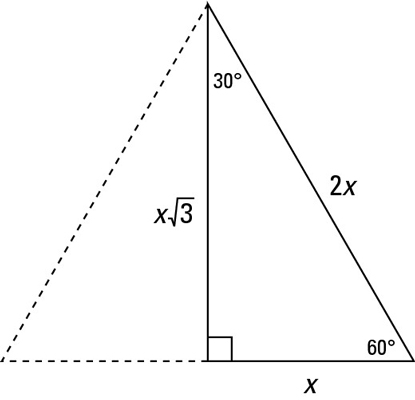
What I want to do in this video is discuss a special class of triangles called triangles and I think you know why they're called this the measures of its angles are 30 degrees 60 degrees and 90 degrees and what we're going to prove in this video this tends to be a very useful result at least for a lot of what you see in a geometry class and then later on in trigonometry class is the ratios between the sides of a triangle that if the hypotenuse has length A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherSolving special right triangles means finding the missing lengths of the sides Instead of using the Pythagorean Theorem, we can use the special right triangle ratios to perform calculations Let's work out a couple of examples Example 1 The longer side of a 30°;



45 45 90 And 30 60 90 Triangles Zona Land Education
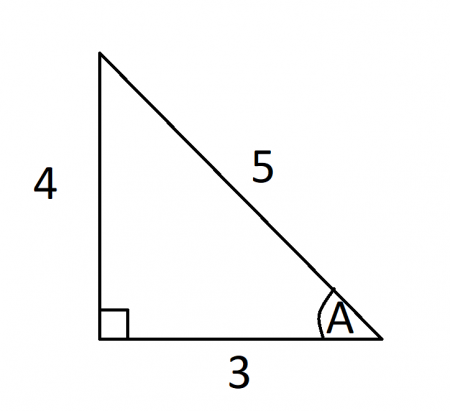



30 60 90 Triangle Formulas Rules And Sides Science Trends
A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other Since the right angle is always the largest angle, the hypotenuse is always the longest side using property 2 We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a2b2=c2 12(3–√)2=13=4=c2 4–√=2=c Next, we can label the length of the new side opposite 30º "a," and add this new mirror image length with the original we had to get, aa=2a If we look at our original 30 60 90 triangle, we now have the following values for each side based on our equilateral triangle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
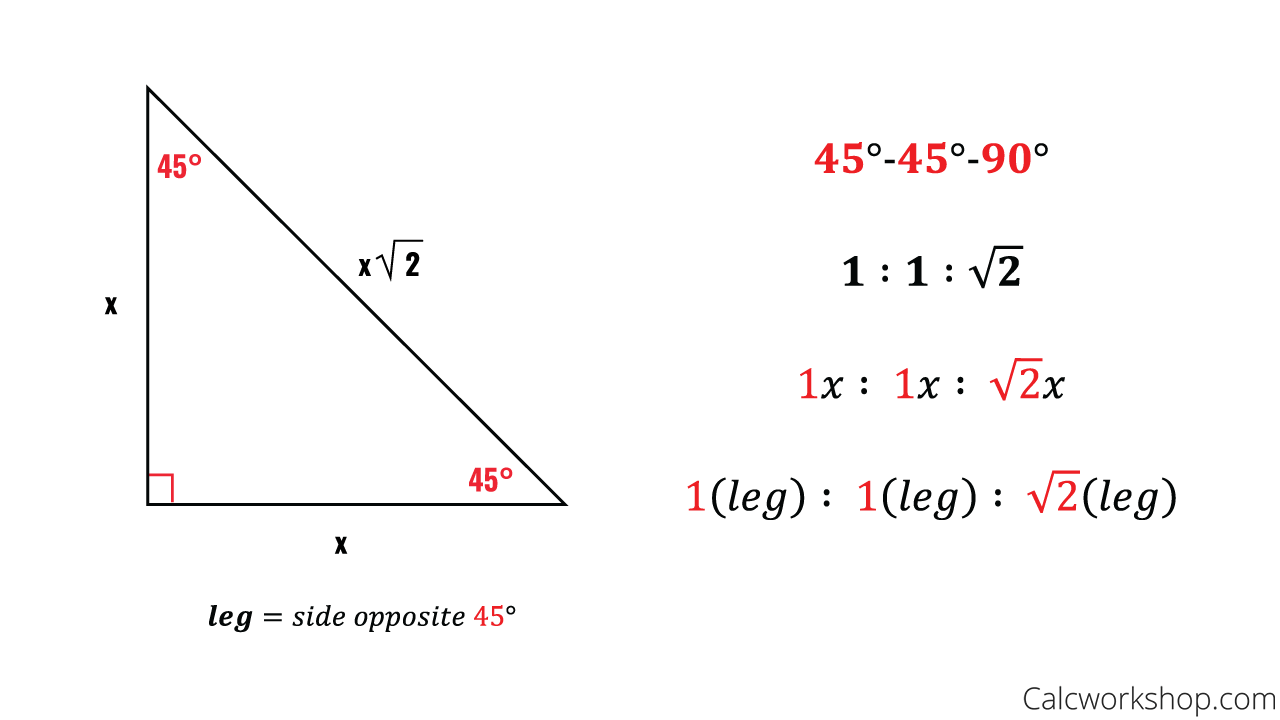



Special Right Triangles Fully Explained W 19 Examples
A triangle is a triangle whose angles of 30º, 60º, and 90º The lengths of the sides of a triangle are always in a fixed ratio Suppose the short leg, opposite the 30º angle, has length x Then the hypotenuse has length 2x, and the long leg, opposite the 60º degree angle, has length (sqrt 3)x The sides of every triangle will have this 1 2 sqrt(3) ratioIn a triangle, the ratio of the sides is always in the ratio of 1√3 2 This is also known as the triangle formula for sides yy√32y Let us learn the derivation of this ratio in the triangle proof section The triangle ratio for the length of the sides is as follows The hypotenuse is twice the shorter leg The longer leg is {eq}\sqrt{3} {/eq} times the shorter side




30 60 90 Triangle Theorem Ratio Formula Video
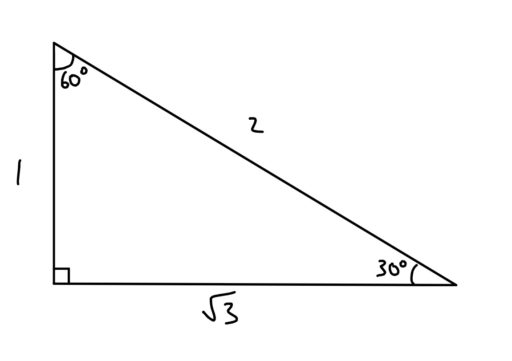



Appendix All The Formulas
30 60 90 and 45 45 90 Triangle Calculator I N S T R U C T I O N S Start by entering the length of a triangle side Then click on which type of side it is The 5 choices you have are As soon as you click that box, the output boxes will automatically get filled in by the calculator Clicking "RESET" clears all of the boxesThe property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5 The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Sides Examples Angles Full Lesson
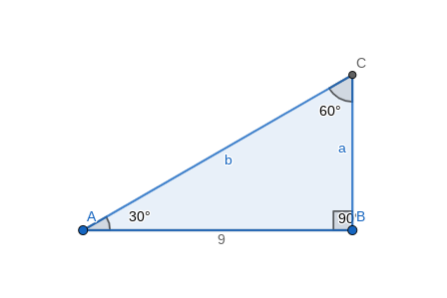



Activity 22 Construct A 30 60 90 Triangle Geogebra




Hints For Problem 5 To Find The Height Of An Chegg Com
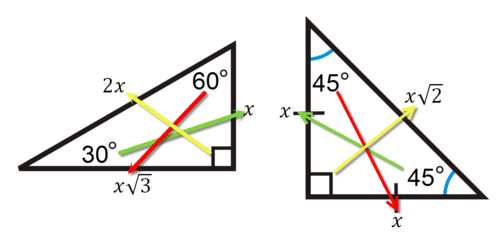



Special Right Triangles Read Geometry Ck 12 Foundation
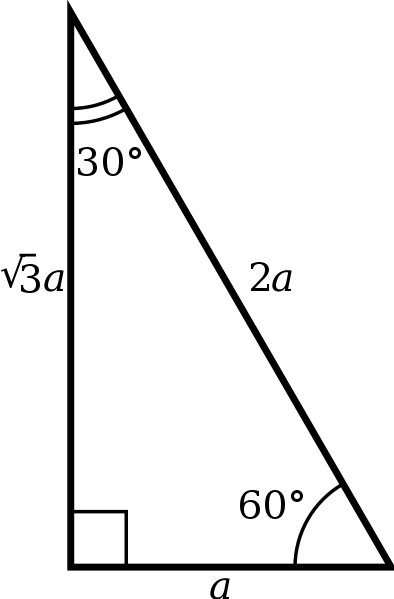



30 60 90 Triangle Formulas Rules And Sides Science Trends



The Easy Guide To The 30 60 90 Triangle




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangles Spock S Guide To Math 4



A 30 60 90 Triangle




30 60 90 Triangle Definition Theorem Formula Examples



Solve A 30 60 90 Triangle With Gradea



What Is The Ratio Of Sides Of A Triangle If The Angles Are 30 60 90 Quora




A Quick Guide To The 30 60 90 Degree Triangle Dummies



30 60 90 Triangle Definition Theorem Formula Examples



1




Instructions Use The Ratio Of A 30 60 90 Triangle To Solve For The Variables Leave Your Answers As Brainly Com




30 60 90 Triangle Calculator Formula Rules



The Easy Guide To The 30 60 90 Triangle



9 7 Special Right Triangles Objective After Studying This Section You Will Be Able To Identify The Ratio Of Side Lengths In A 30 60 90 Triangle And Ppt Download



30 60 90 Triangle Rules




Special Right Triangles




The Complete Guide To The 30 60 90 Triangle




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation



What Is The Ratio Of Sides Of A Triangle If The Angles Are 30 60 90 Quora



30 60 90 Special Triangles Geometry Mathsux 2
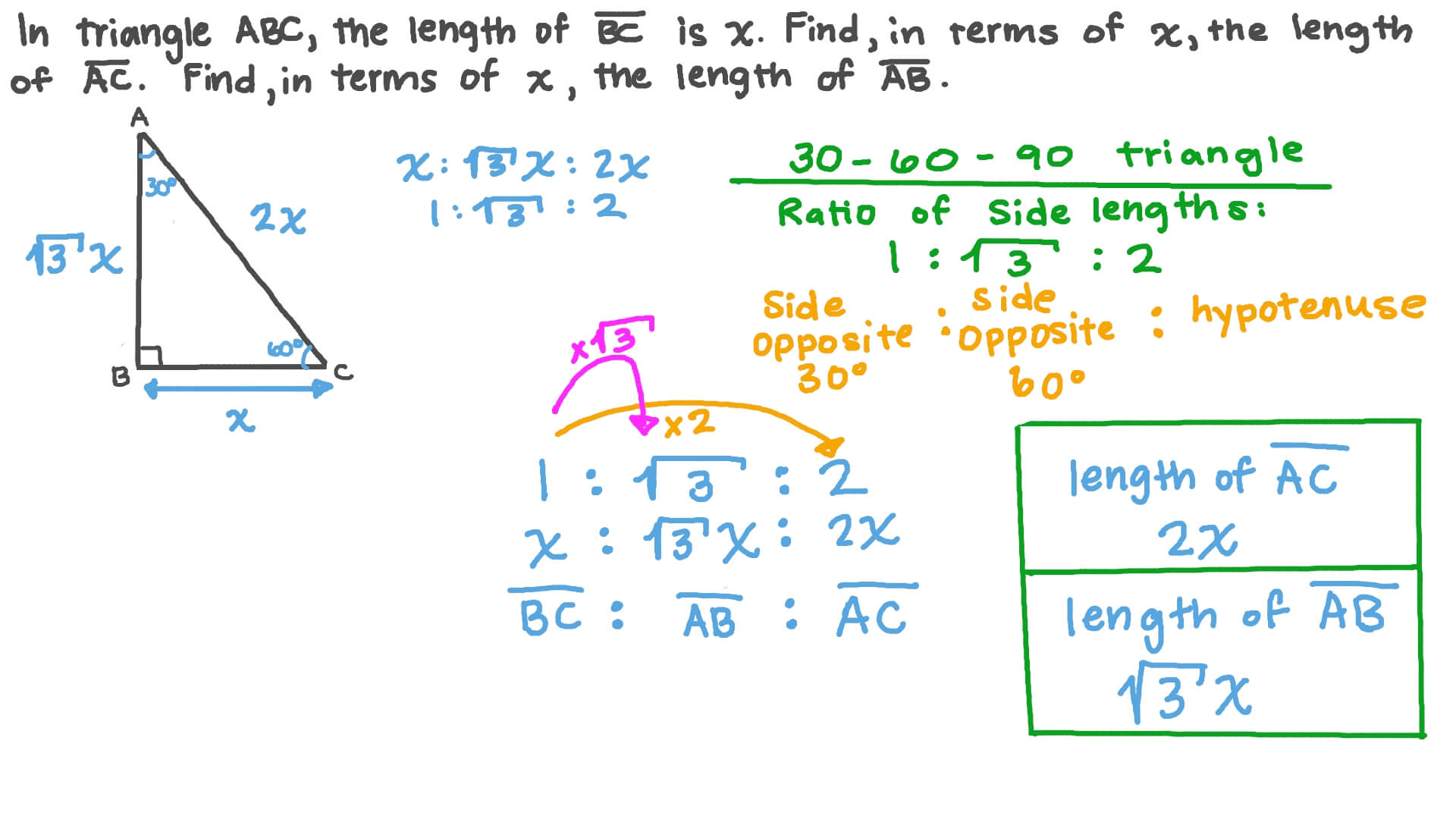



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangles Special Right Triangle Trigonometry Youtube




Special Right Triangles



1




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Proof Don T Memorise Youtube




30 60 90 Triangle Definition Theorem Formula Examples



What Are The Side Relationships Of A 15 75 90 Triangle Quora




30 60 90 Triangle Identity Gmat Geometry Apex Gmat Blog




The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Definition Theorem Formula Examples




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 45 45 90 Special Right Triangles Youtube




Solved Question 6 What Is The Ratio Of The Side Lengths Of A Chegg Com




The 30 60 90 Triangle Topics In Trigonometry
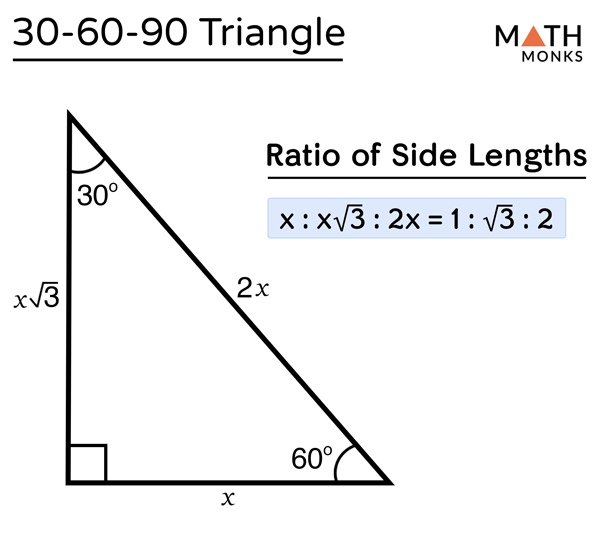



30 60 90 Triangle Definition Formulas Examples




Which 30 60 90 Degree Triangle Is Labeled With The Correct Side Length Ratio Brainly Com




30 60 90 Triangles
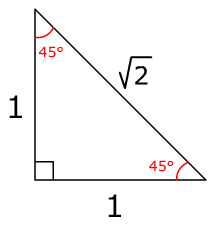



45 45 90 Right Triangle Side Ratios Expii




Conquering Right Triangles The Pythagorean Theorem On Act Math Part 1 Magoosh Blog High School




Velocity



1




Special Right Triangles Review Article Khan Academy



Right Triangles Gmat Free
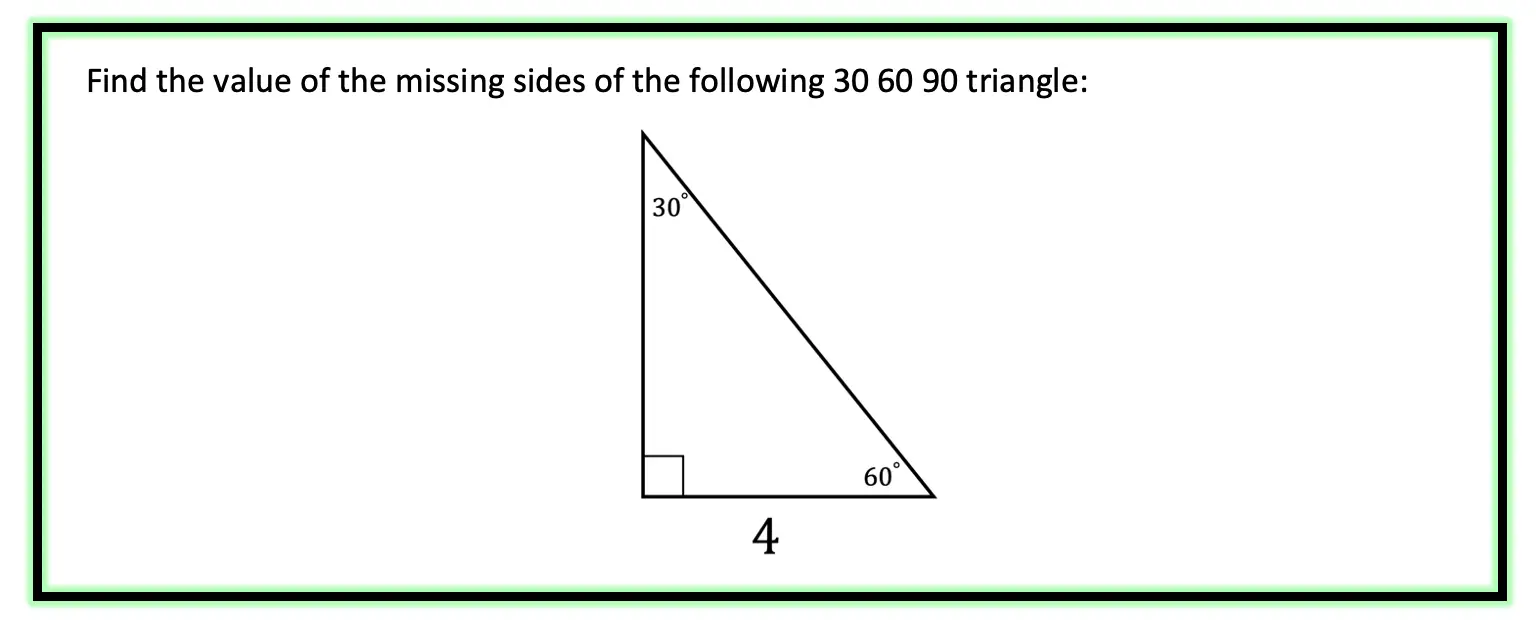



30 60 90 Special Triangles Geometry Mathsux 2
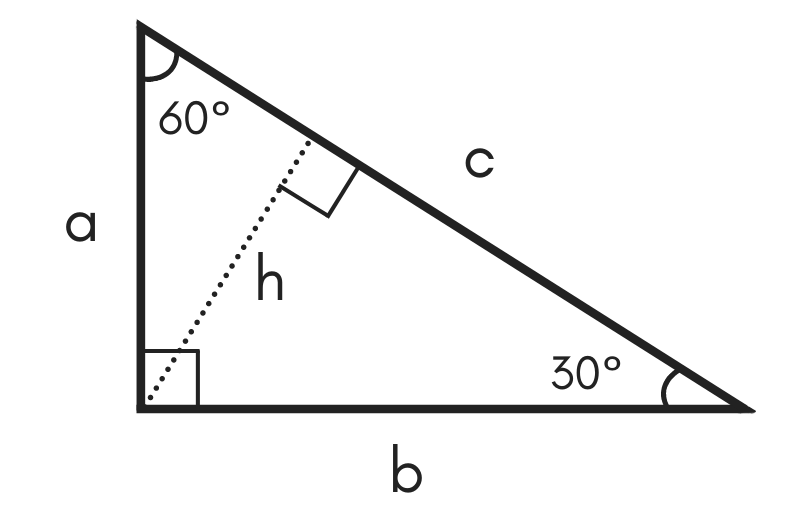



30 60 90 Special Right Triangle Calculator Inch Calculator




Which 30 60 90 Degree Triangle Is Labeled With The Correct Side Length Ratio Brainly Com




The 30 60 90 Triangle Topics In Trigonometry




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




Solved Deriving The Ratio Of The Sides Of A 30 60 90 Chegg Com



Right Triangles Gmat Free



A 30 60 90 Triangle Math Central



Special Right Triangle 30 60 45 45 37 53 Elearning




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Calculator Formula Rules




Learn About The 30 60 90 Triangle Caddell Prep Online




The Side Lengths Of A 30 60 90 Triangle Are In The Ratio 1 3 2 What Is Sin 30 Brainly Com




30 60 90 Triangle Theorem Ratio Formula Video




The Side Lengths Of A 30 60 90 Triangle Are In The Ratio 1 3 2 What Is Sin 30 Brainly Com




A Quick Guide To The 30 60 90 Degree Triangle Dummies



1




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




How To Use The Special Right Triangle 30 60 90 Studypug




Velocity
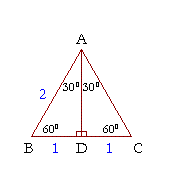



30 60 90 Right Triangle Side Ratios Expii
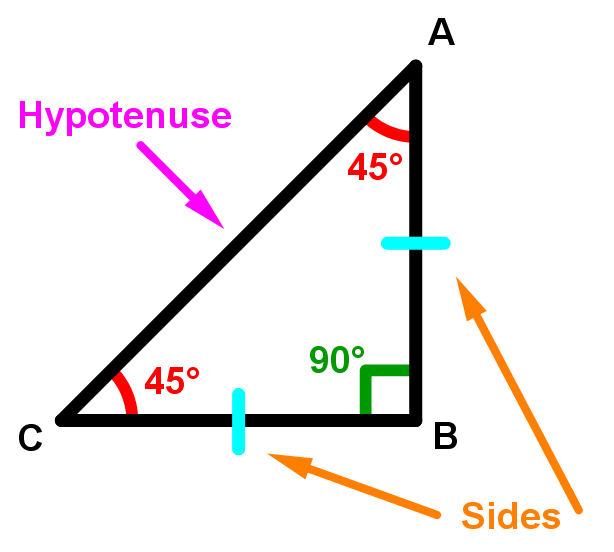



How To Use The Special Right Triangle 45 45 90 Studypug
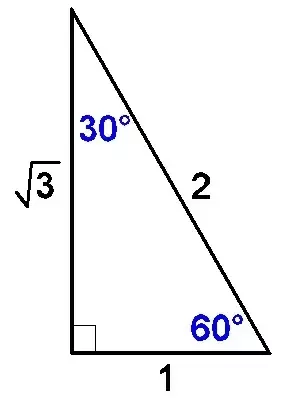



30 60 90 Right Triangle How Do I Solve If The Long Leg Is 10 Socratic




How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Explanation Examples



The Easy Guide To The 30 60 90 Triangle




Special Right Triangle Wikipedia
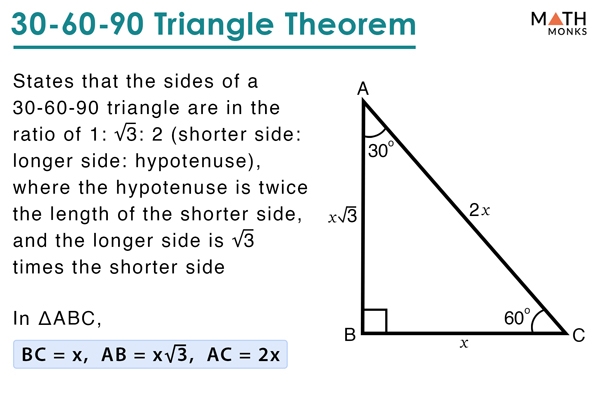



30 60 90 Triangle Definition Formulas Examples



0 件のコメント:
コメントを投稿